10 dedos en las manos
El motivo histórico para utilizar el sistema decimal es que disponemos de 10 dedos en las manos y contamos así por herencia del antiguo Egipto, aunque no todas las culturas han contado en base 10. Los sumerios contaban en un sistema en base 60 (que es múltiplo de 12) e incluso actualmente contamos el tiempo y los ángulos en sistemas referenciados al duodecimal.
 |
| Al igual que en la antigua Mesopotamia, podemos usar los dedos de las manos para contar en base 12 - Foto vía Dozenalism - |
En nuestro sistema decimal utilizamos 10 símbolos diferentes -del 0 al 9- para representar cualquier número. En el sistema duodecimal hay que utilizar 12 de ellos -contamos del 0 al 11- por lo que de entrada debemos añadir dos nuevos números a nuestra forma de contar. Sin embargo no hay aun un estándar que defina que dos símbolos se añaden al sistema. Históricamente se ha utilizado para el 10=X y para el 11=E siendo la letra X parecida a la letra Ji griega en minúscula y se pronuncia "dek" y la letra E como el número 3 al revés pronunciándose "el". Otros cambian la X (Ji griega) por un 2 al revés tal como se ve en la imagen superior. Otro sistema usado es el 10=A y el 11=B, pero la Dozenal Society of America aboga por los símbolos para el 10=* y 11=#.
Los 12 símbolos del sistema duodecimal serían por tanto: 0,1,2,3,4,5,6,7,8,9,*,#
Aritmética más sencilla
Los defensores del sistema duodecimal argumentan que la aritmética resulta más sencilla usando esta base. Mientras que el número 10 tiene sólo 2 factores propios (sin contar el 1 y el mismo número 10): el 2 y el 5, el 12 tiene 4 factores propios: el 2, 3,4 y 6. Debido a esto, las multiplicaciones y las divisiones duodecimal son más sencillas y por tanto muestra ser un sistema más eficiente.
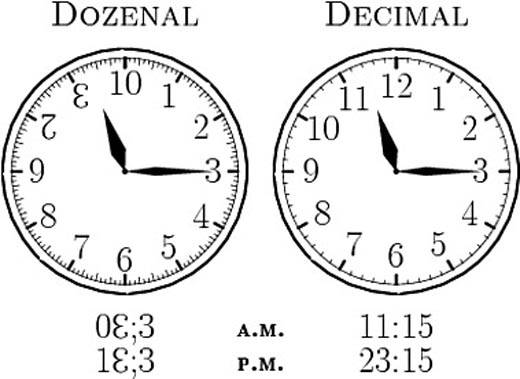 |
| Relojes en el sistema decimal y duodecimal - Foto vía The Guardian - |
El sistema es muy sencillo de usar cuando pensamos por ejemplo en tercios y cuartos. Representemos 1/3, 1/4, 1/2 y 1/6 en los sistemas decimal y duodecimal:
(Decimal) 1/3 = 0,3333333...
(Duodecimal) 1/3=4/10=0,4
(Decimal) 1/4=0,25
(Duodecimal) 1/4=3/10=0,3
(Decimal) 1/2=0,5
(Duodecimal) 1/2=6/10=0,6
(Decimal) 1/6=0,1666666...
(Duodecimal) 1/6=2/10=0,2
Usar el sistema duodecimal en matemáticas complejas no va a suponer ninguna diferencia con el decimal, pero dado que de forma natural -en el día a día- solemos fraccionar en la mitad, en tercios, cuartos... el sistema duodecimal presenta una clara ventaja en este tipo de operaciones sobre el sistema decimal.
Enlaces de interés:
Conversor sistema decimal/duodecimal
The Dozenal Society of Great Britain
The Dozenal Society of America
Adeptos al sistema duodecimal en Facebook

No hay comentarios:
Publicar un comentario
Nota: solo los miembros de este blog pueden publicar comentarios.